PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法,是基于变量协方差矩阵对数据进行压缩降维、去噪的有效方法,PCA 的思想是将 n 维特征映射到 k 维上(k < n),这 k 维特征称为主元,是旧特征的线性组合,这些线性组合最大化样本方差,尽量使新的 k 个特征互不相关。
相关概念
协方差(Covariance)
协方差是描述不同变量之间的相关关系,协方差>0 时说明 X 和 Y 是正相关关系,协方差<0 时 X 和 Y 是负相关关系,协方差为 0 时 X 和 Y 相互独立。
协方差的计算是针对两维的,对于 n 维的数据集,可以计算 C(n,2)种协方差。
例如对于三维(x,y,z),其协方差矩阵如下,可看出协方差矩阵是一个对称矩阵(symmetrical),其对角线元素为每一维的方差: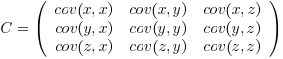
特征值和特征向量
A 是 n 阶方阵,如果存在数 m 和非零 n 维列向量 x,使得 Ax=mx 成立,则称 m 是矩阵 A 的一个特征值,向量 x 是矩阵 A 的特征向量。
PCA
问题引入
对于正交属性空间中的样本点,如何使用一个超平面对所有的样本进行恰当的表达?
目标
能够达到要求的超平面大概应该具有这样的性质:
- 最近重构性:样本点到这个超平面的距离都足够近。
- 最大可分性:样本点在这个超平面上的投影点能尽可能分开。
有趣的是:
基于最近重构性和最大可分性,能分别得到主成分分析的两种等价推导。
从最近重构性出发,PCA 优化目标为: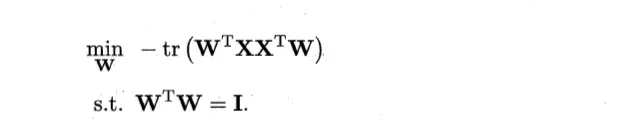
从最大可分性出发,PCA 优化目标为: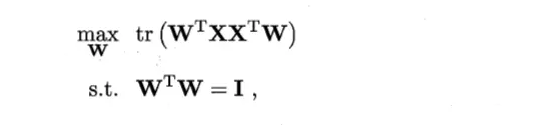
显然,上述两个优化目标是等价的。
因此,只需对协方差矩阵进行特征值分解,将求得的特征值排序即可。
算法步骤
- 去掉数据的类别特征(label),将去掉后的 d 维数据作为样本
- 计算 d 维的均值向量(即所有数据的每一维向量的均值)
- 计算所有数据的协方差矩阵(或者散布矩阵)
- 计算特征值(e1,e2,…,ed)以及相应的特征向量(lambda1,lambda2,…,lambda d)
- 按照特征值的大小对特征向量降序排序,选择前 k 个最大的特征向量,组成 d*k 维的矩阵 W(其中每一列代表一个特征向量)
- 运用 d*K 的特征向量矩阵 W 将样本数据变换成新的子空间。(用数学式子表达就是,其中 x 是 d*1 维的向量,代表一个样本,y 是 K*1 维的在新的子空间里的向量)
算法描述
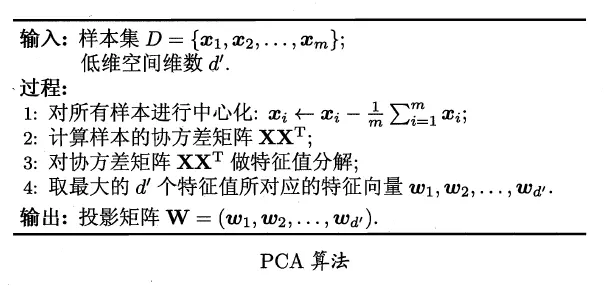
算法评价
降维后低位空间的位数 d’通常由用户事先指定,或通过在 d’值不同的低位空间中对 k 近邻分类器进行交叉验证来选取较好的 d’值。对于 PCA,还可从重构角度设置一个重构阈值。
此外,低维空间与原始高位空间必有不同。这是降维导致的结果,舍弃这部分信息也是必要的:
- 一方面,舍弃这部分信息之后能使样本的采样密度增大,这正是降维的重要动机。
- 另一方面,当数据受到噪声影响时,最小的特征值对应的特征向量往往与噪声有关,将他们舍弃可以在一定程度上起到去噪的效果。



如果长时间无法加载,请针对 disq.us | disquscdn.com | disqus.com 启用代理