LeetCode84.LargestRectangleInHistogram

题目概述

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

题目大意

给定 n 个非负的整数，代表柱状图中的每一个柱形的高度，每个柱形的宽度固定并且都为 1，找出这个柱状图中面积最大的矩形，输出这个最大的面积值。

示例

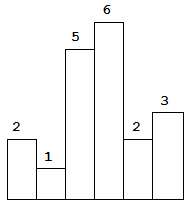
如上图所示是一个单位宽度为 1 的柱状图，给定的高度数组为：[2,1,5,6,2,3]

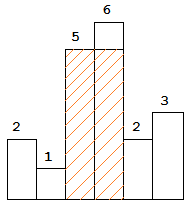
面积最大的矩形如上图阴影所示，并且面积为 10。

Input: [2,1,5,6,2,3]
Output: 10

解答

尝试一

定义 front 和 rear 首尾两个标记，分别从两侧向中间移动。

每次寻找当前数组中最小的高度，乘以当前长度，更新最大值。
比较首尾标记，将两者中较小的向中间移动一步，进行下一步迭代。

很遗憾！这种方法是错误的。可以通过下面的 case 判断：

[5,5,1,7,1,1,5,2,7,6]
63 / 96 test cases passed.

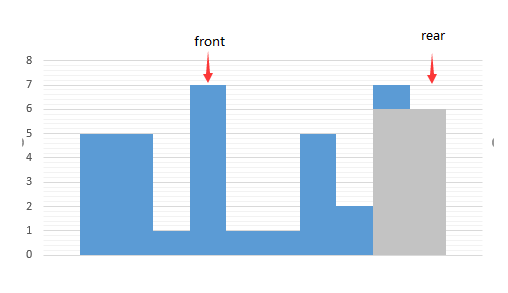
当前情况下，rear 会向左移动，而这样则无法得到图中灰色部分的最大面积矩形。

尝试二

从两侧考虑失败后，考虑选择最高的，选择两侧相对高者，向两侧扩展，知道遍历整个柱状图。
但是这种情况需要考虑最高者，存在多个。则需要格外的比较步骤，代价更大。

这样考虑，遍历一遍数组，对于每个元素，寻找当前元素两侧，比该元素小的元素，则以当前元素高度，所能构成的矩形面积为：

height[i] * (lessFromRight[i] - lessFromLeft[i] - 1)

其中 lessFromLeft 和 lessFromRight 分别第 i 个元素左右两侧比 i 更小的元素的索引。因此，

for(let i = 0 ;i < len; i++){
    max = Math.max(max, heights[i] * (lessFromRight[i] - lessFromLeft[i] - 1))
}

那么记下来的问题就是如何高效的计算出每个元素的 lessFromLeft 和 lessFromRight。例如在寻找 lessFromLeft 时：

for (let i = 1; i < height.length; i++) {
    let p = i - 1;
    while (p >= 0 && height[p] >= height[i]) {
        p--;
    }
    lessFromLeft[i] = p;
}

这样的方法的时间复杂度会达到 O(n^2),这里考虑使用动态规划进行优化。因为我们并不需要扫描每一个元素直到左侧，可以使用之前已经得到的 lessFromLeft 的结果。那么：

for (let i = 1; i < height.length; i++) {
    let p = i - 1;
    while (p >= 0 && height[p] >= height[i]) {
        p = lessFromLeft[p];
    }
    lessFromLeft[i] = p;
}

最后的结果是：

Runtime: 60 ms, faster than 93.86% of JavaScript online submissions for Largest Rectangle in Histogram.
Memory Usage: 38.5 MB, less than 20.40% of JavaScript online submissions for Largest Rectangle in Histogram.

相关代码在这里。